AES

Introduction

最为“可靠”的对称加密算法
WinRAR，7-zip 加密文件时用的就是 AES
勒索软件用的也是 AES 算法加密（使用 RSA 传递密钥）

Format

明文长度=16byte，密文长度=16byte
AES 的 key 有三种规格，分别为 (16byte，24byte,32byte)

Encryption

unsigned char a[4] = {0x03, 0x01, 0x01, 0x02}; 
AddRoundKey(p, k);  // 圈密钥加法运算 result = p ^ k 
                    // (在GF(2^8)中加法等价于异或)
for(i=1; i<=10; i++) { 
	ByteSub(p, 16); // sbox字节替换 p[i] = sbox[p[i]]; 
	// 在ShiftRow之前，p要进行行列变换
	ShiftRow(p); // 逐行进行循环位移
	if(i != 10) // MixColumn，多项式乘法
		MixColumn(p, a, 1); /* do mul */ 
	else MixColumn(p, a, 0); /* don't mul */ 
	AddRoundKey(p, k+i*(4*4)); 
}

在 ShiftRow 之前进行行列表换主要是为了方便后续的 MixColumn 运算 (ShfitRow 本身要和 MixColumn 结合)

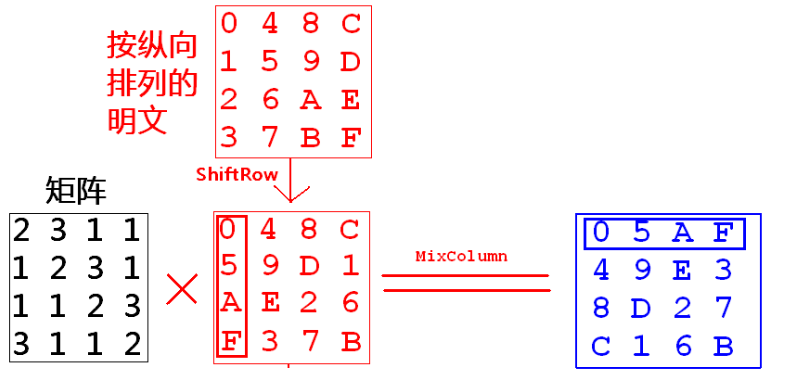
如果不在 ShiftRow 之前进行行列转换，在 MixColumn 中计算会比较复杂

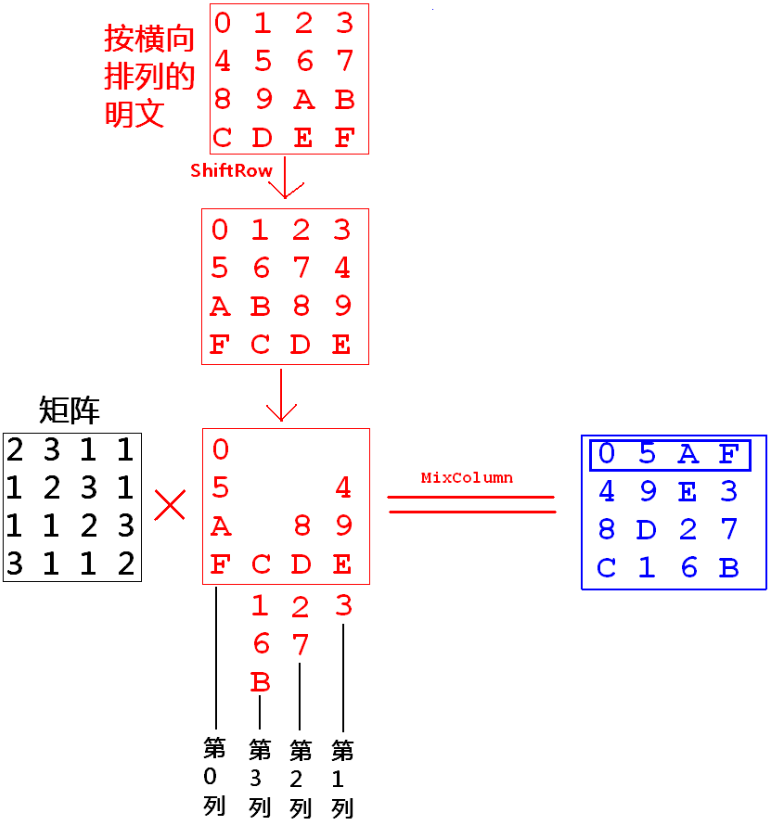
MixColumn

多项式乘法 (一次加密 4byte，1byte 表示一个多项式系数)
例： $(3 x^{3} + x^{2} + x + 2) * (a_{3} x^{3} + a_{2} x^{2} + a_{1} x^{1} + a_{0} x^{0}) \mod (x^{4} + 1)$
被乘数 $3 x^{3} + x^{2} + x + 2$ 给定，在 $x^{4} + 1$ 下不可约，其乘法逆元为 $B x^{3} + D x^{2} + 9 x + E$ （若 $3 x^{3} + x^{2} + x + 2$ 不可约，则 $x^{4} + 1$ (可拆分为 $(x^{2} + 1)^{2}$ ), $3 x^{3} + x^{2} + x + 2$ 可能不互素）

本身的乘法
1. 总流程
2. 高次系数在下，低次系数在上，进行矩阵乘法
3. 左乘的矩阵，因为原多项式 $(3 x^{3} + x^{2} + x + 2)$ 给定，所以该矩阵也固定不变
系数的运算
1. 加法使用异或
2. 乘法使用农夫算法 (使得结果仍为 1byte)

农夫算法

target: $x (8 b i t) * y (8 b i t) \mod 11 B h = z (8 b i t)$

int z = 0;
while(y){// 类似快速幂
	if(y&1){
		z = z ^ x;
	}
	x <<= 1;
	y >>= 1;
	if(x & (1<<8)){
		x = x ^ 0x11B // x = x - 11B 因为在GF(2^8)中，11B+11B=11B^11B=0
	}
}

Sbox 生成

sbox[a] =(( $a^{- 1}$ * 0x1F) mod ( $X^{8}$ + 1)) ^ 0x63;

轮密钥生成

以最初的 4byte 密钥作为种子密钥，每轮生成 4byte 新密钥，共进行 10 轮

k[4] = k[3]
k[4:7] 循环左移 1byte
k[4:7] 在 sbox 中替换
k[4] ^= r (r = $2^{(i - 4) / 4}$ mod 0x11B)
k[4] ^= k[0]
k[5] = k[4] ^ k[1]；k[6] = k[5] ^ k[2]；k[7] = k[6] ^ k[3]；

Math

$G F (2)$

加法等效于异或
0+1=1,1+0=1,0+0=0,1+1=0

$G F (2^{8})$

加法按位加法 (异或)，不进位
00110111+00001111=00111000
任意一个数的相反数就是它本身
00110111+00110111=00000000

AES