Turing Machine
图灵机定义
图灵机的运行规则
- 图灵机由 有穷状态控制器 和 带 组成,两者之间通过带头进行操作
- 控制器在每步完成两个功能
- 让控制器进入新状态(和 DFA / NFA 类似)
- 在当前扫描的带方格中 填入 一个符号 / 把读写头向左或向右 移动 一个带方格
图灵机的符号标示
A Turing Machine is 5-tuple
: a finite set of state : an alphabet (containing and ) : initial state : a set of halting state : transition function is current state is symbols is next state is writing or moving
- it satisfying
- for any
, for some - for any
, any , if ,
- for any
图灵机的当前状态可表示为
- 带内容的简化记号
: 表示 里的带内容
A configuration is a member of
- writing:
, , , - moving left:
, and - moving right:
, ,
Similarly, we have the.
- formal definition
- Implemental-level description(diagram)
- high-level description "pseudo code"
图灵机的记号
- 基本机器
- 写符号机
:对每个 , - 移带头机
,
- 写符号机
- 组合机器:直到上一台机器停机为止才应用从前一台机器到后一台机器的连接
flowchart LR M1 --a--> M2 M1 --b--> M3
- 更多机器
: can becomes simply , or even : 寻找当前扫描方格右方的第一个空格方格 : 寻找当前扫描方格左方的第一个空格方格 : 寻找当前扫描方格右方的第一个非空格方格 : 寻找当前扫描方格左方的第一个非空格方格 : transforms into , where contains no blanks. : into , where contains no blanks.
If
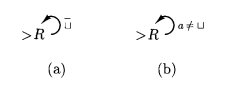
图灵机的应用
Recoganize Language 识别语言
Let
- for every
, , accepts - for every
, , rejects
A language
we can said that M semidecides L(M)
graph s(semidecide) --> re(recursively enumerable) re --> s d(decide) --> rl(recurive language) rl --> d rl --充分条件--> re subgraph 决定 s d end
Let
Construct
- for i = 1, 2, 3, ...
- for s =
, , , ... - run
on for steps - if
halts on within steps - halt
- run
- for s =
PS: 这是一种常用的技巧:限制每次的运行步数,不断 扩散
Compute function 表示函数
Let
Now let
- 证明 recursive
- 定义法:构造对应的 TM
- 归约法:
known recursive language
- 证明 recursively enumerable
- 定义法:构造对应的 TM
- 归约法:
known recursively enumerable language
- 证明 non-recursive
- 归约法:known recursively enumerable language
- 归约法:known recursively enumerable language
- 证明 not recursively enumerable
- If
and is recursively enumerable, then is recursive - 归约法:known not recursively enumerable language
- If
is not recursive enumerable
is not recursive enumerable
is not recursive enumerable
- try
with input 'M''w', with input does not halt on iff halts on every input - Construct
= on input v - run
on for steps - if
halts on within steps - loop(not halts)
- if
does not halts on within steps - halts
- run
- Validation
not halts on ⇒ halts on every input halts on ⇒ when is long enough, f loop ⇒ does not halt on every input
拓展图灵机
所有的拓展图灵机都可以等价转换成普通图灵机
- multiple tapes
- two-way infinite tape
- multiple heads
- two-dimensional tape
- random access
- non-determinstic turing machine
a non-deterministic Turing Machine (NTM) is 5-tuple
A NTM
iff - if
some branch halts - if
no branch halts
A NTM
- there is a natrual number
, depending on and such that there is no configuration satisfying iff