时域与频域
- 时域:描述数学函数或物理信号对 时间 的关系
- 频域:描述信号在频率方面特性时用到的坐标系
频域
- 幅频图 & 相频图
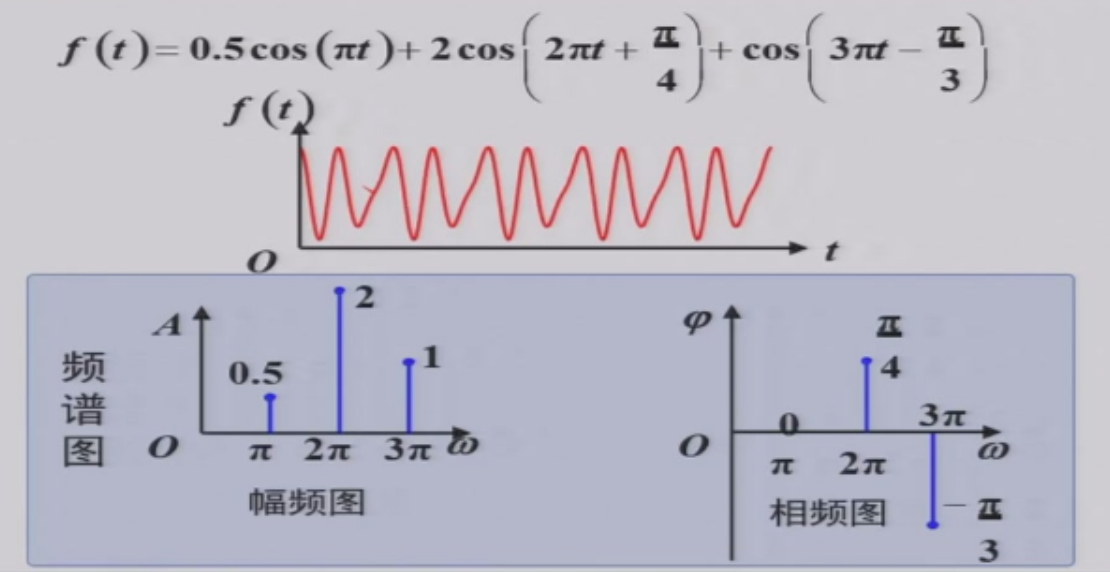
- 周期信号可以被分解为 直流分量 和 不同频率的余弦分量
- 周期信号也可以被分解为不同频率的 虚指数信号
- 傅里叶变换 是时域与频域相互转换的重要数学基础
短时傅里叶变换
短时傅里叶变换 STFT(Short-time Flourier Transform) 是和 傅里叶变换 相关的一种数学变换,其运算步骤如下所示:
- 将长时间信号分成无数个较短的等长信号(加窗)
- 计算每段的傅里叶变换
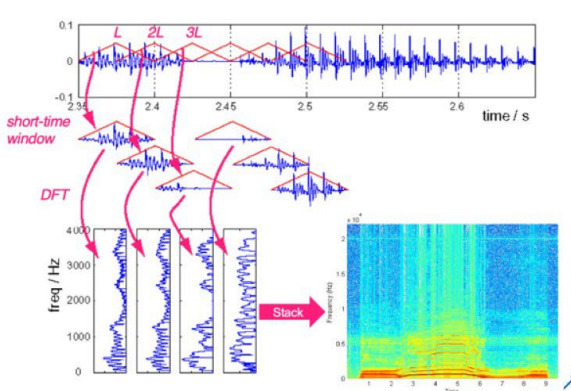
其数学公式如下所示:
是时间帧索引 是帧移大小 是谐波频率
小波变换
小波变换通过替代傅里叶变换的三角函数基为小波基实现。
小波基
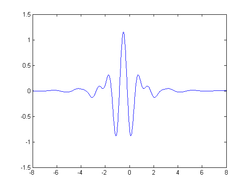
相较于傅里叶变换,小波变换
- 既具有 频率分析 的性质,又能表示 发生的时间,有利于分析确定时间发生的现象。
- 小波变换的 多分辨率 的变换,有利于各分辨率不同特征的提取
- 对于突变信号,小波变换只在有限的 局部 内会对它产生响应,对于整体的分析相较于傅里叶变换更小