毫米波感知

毫米波简介

应用场景
- 自动驾驶（汽车雷达：障碍物检测、测速）
- 工业控制（震动检测、水位检测）
- 智能家居（手势检测、摔倒检测）
功能上
- 波长短，空间分辨率高
- 具有一定穿透性
物理实现：天线小、体积小、集成度高
劣势
- 易衰减，感知距离受限
- 绕射能力弱

FMCW 毫米波雷达

Frequency-Modulated Continuous-Wave 调频连续波，又称 Chirp 信号（“啁啾信号”），其信号的频率随时间呈线性变化。
其频率变化的图像如下图所示：

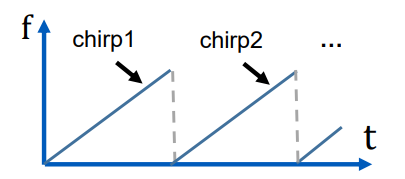
其频率的数学表达式为 $f_{T} (t) = f_{c} + \frac{B}{T_{c h i r p}} t$ ，其中 $B$ 为带宽， $T_{c h i r p}$ 为 Chirp 信号的时长， $f_{c}$ 为起始频率。

拍频信号

FMCW 毫米波雷达的可以通过对接收信号和发送信号的处理，获得拍频信号，进一步获取物体的距离、速度等信息。其流程如下图所示：

flowchart LR
接收信号 --> HPQ((混频器)) --> 低通滤波器 --> ADC --> 拍频信号
发送信号 --> HPQ

混频器的作用是将接收信号 $x_{1}$ 和 $x_{2}$ 相乘，变为 $x_{o u t} = x_{1} \cdot x_{2}$ 输出
低通滤波器将会过滤掉 $| f_{1} + f_{2} |$ 的信号，仅保留 $| f_{1} - f_{2} |$ 部分

获取拍频信号的数学原理如下所示：

\begin{aligned} x_{1} = \sin (2 π f_{1} + ϕ_{1}), x_{2} = \sin (2 π f_{2} + ϕ_{2}) \\ x_{1} \cdot x_{2} = \frac{1}{2} \cos [2 π (f_{1} - f_{2}) t + (ϕ_{1} - ϕ_{2})] - \frac{1}{2} \cos [2 π (f_{1} + f_{2}) t + (ϕ_{1} + ϕ_{2})] \end{aligned}

故拍频信号可表达为 $x_{o u t} = \sin (2 π f_{0} t + ϕ_{0})$ ，其中 $f_{0} = f_{1} - f_{2}$ ， $ϕ_{0} = ϕ_{1} - ϕ_{2}$

距离感知

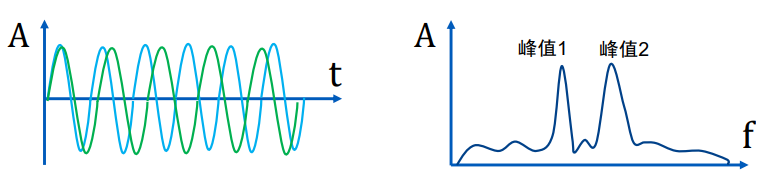
某物体的距离可通过拍频信号的频率获得

\begin{aligned} d = \frac{c (f_{1} - f_{2})}{2 S} \\ 其 中 S = \frac{B}{T_{c h i r p}}, c 为 光 速 \end{aligned}

当存在多个物体时，拍频信号的频谱将出现多个峰值，分别代表不同的物体。

速度感知

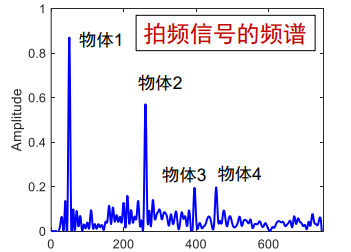
物体运动的速度可以通过计算 相邻 Chirp 信号 所对应的拍频信号的 相位变化 得到

\begin{aligned} ϕ_{0} = ϕ_{1} - ϕ_{2} = 2 π f_{c} τ = 2 π \frac{c}{λ} \cdot \frac{2 d}{c} = \frac{4 π d}{λ} \\ 其 中 λ 为 起 始 频 率 f_{c} 对 应 的 波 长 \\ 两 个 间 隔 C h i r p 信 号 的 相 位 变 化 Δ ϕ = \frac{4 π Δ d}{λ} \\ ∴ \frac{Δ ϕ}{T_{c h i r p}} = \frac{4 π}{λ} \cdot \frac{Δ d}{T_{c h i r p}} = \frac{4 π}{λ} v \\ ∴ v = \frac{λ Δ ϕ}{4 π T_{c h i r p}} \end{aligned}

拍频信号数字处理

在通过 ADC 将模拟信号经过采样转为数字信号后，需要进行进一步的处理。

flowchart LR
	ADC --> 拍频信号 --> R(Range FFT)
	拍频信号 --> D(Doppler FFT)
	拍频信号 --> A(Angle FFT)

每个拍频信号都是由若干 采样点 构成的，每个周期的拍频信号也对应着一个 采样序列。在采样若干周期后，就可以获得下方矩阵形式的数据用于后续处理。

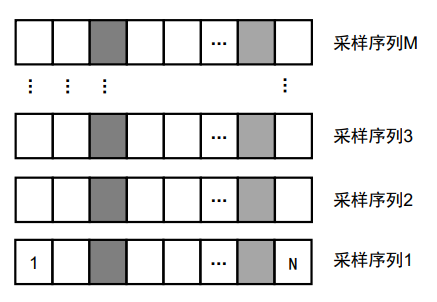
共 M 段采样序列，每段共有 N 个采样点，构成 $M \times N$ 大小的矩阵

Range FFT

对每段采样序列上的 N 个采样点进行傅里叶变换，得到不同的频率成分，每一种频率都对应一种距离。同时距离可以被还原到采样点中，因为相同距离对应的采样点也相同。

Doppler FFT

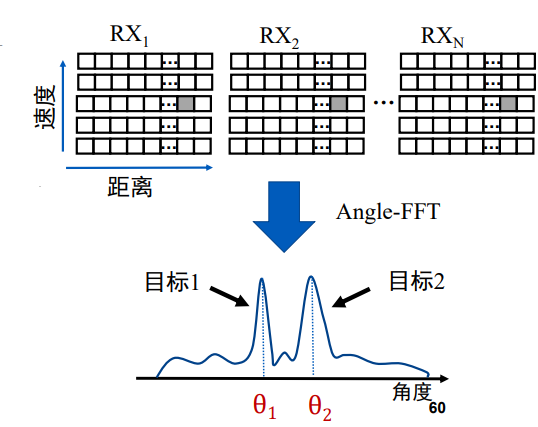
对相同距离的物体进行速度分析：对列进行傅里叶变换，得到不同的频率成分，每一种频率都对应一种速度。

Rangle FFT 和 Doppler FFT 合称为 2D-FFT，但其无法区分相同距离且速度相近的多个目标，故引入方位角，通过 Angle FFT 辨别。

Angle FFT

波达角：回波与雷达天线平面的夹角 $θ$
波达角可通过设置多个天线，求取不同天线的 2D-FFT 结果相应位置的相位差，根据波达角计算公式，获取物体的角度。波达角计算公式如下图所示；

\begin{aligned} Δ ϕ = \frac{2 π Δ d}{λ}, Δ d = L \sin θ \\ Δ ϕ = \frac{2 π L \sin θ}{λ} \\ θ = \sin^{- 1} \frac{λ Δ ϕ}{2 π L} \end{aligned}

其中， $L$ 为两天线的间距， $λ$ 为起始频率 $f_{c}$ 对应的波长

波达角分辨率 $Δ θ_{r e s} = \frac{λ}{N L \cos θ}$
雷达的角分辨率和目标的波达角 $θ$ 有关
雷达的接收天线数目越多，角分辨率越精细

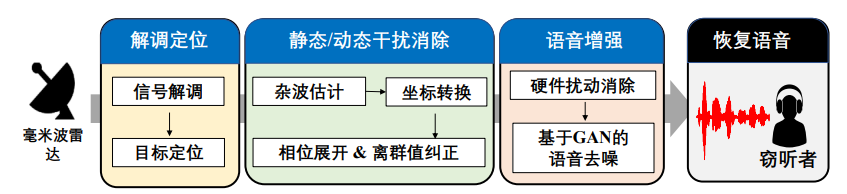
基于毫米波的语音侧信道窃取

Abstract

主要介绍了两个科研结果，分别为 Wavesdropper 和 mmEve

Wavesdropper：基于毫米波的可穿墙讲话人语音检测

原理
- 毫米波可以穿透常用的声学防护材料
- 毫米波短波长可以捕捉到人讲话时声带振动的细粒度信息

mmEve：基于毫米波的远距离手机语音窃听

原理
- 手机听筒在播放音频时，会在手机外壳产生微小振动
- 该振动与所播放音频具有强相关性（振动耦合），可被毫米波设备捕获
步骤
1. 数字化拍频信号
2. Range-FFT
3. 逐点提取相位
4. 相位展开
5. 幅值归一化
6. 手机外壳振动波形