计算理论复习

考点列表

Finite Automata and Regular Languages
- 正则运算及集合的基础知识
- DFA ⇔ NFA ⇔ RL
  - 直接画图
  - RL ⇒ DFA
    - configuration $⊢_{M}$
    - $(K, Σ, δ, s, F)$
  - RL ⇒ NFA
    - $(K, Σ, Δ, s, F)$
  - NFA ⇒ DFA
    - 状态机
  - NFA ⇒ RL
    - NFA 逐步化简
- Regular Languages 的判断
  - 运算闭环 $\cup$ , $\cap$ , $\overset{―}{}$ , $^{\circ}$ , $^{⋆}$
    - 有限个 运算的结合
  - 构造 DFA / NFA
  - Pumping Theorem： $| w | \geq p$ , $w = x y z$
    - $x y^{i} z \in L$
    - $| y | > 0$
    - $| x y | \leq p$
Context Free Language
- CFL ⇒ CFG
  - $(V, Σ, s, R)$
- CFL ⇒ PDA
  - $P = (K, Σ, Γ, Δ, s, F)$
- CFG ⇒ PDA
  - $s$ ⇒ $((p, e, e), (q, s))$
  - $A \to u$ ⇒ $((q, e, A), (q, u))$
  - $a \in Σ$ ⇒ $((f, a, a), (f, e))$
- CFL 的判断
  - 运算闭环 $\cup,^{*},^{\circ},^{R}$ ；不闭环 $\overset{―}{}, \cap$
    - CFL $\cap$ RL = CFL
  - 构造 CFG / PDA
  - Pumping Theorem: $| w | \geq p$ , $w = u v x y z$
    - $u v^{i} x y^{i} z \in L$
    - $| v | + | y | > 0$
    - $| v x y | \leq p$
- *CNF
  - $s \to e$
  - $A \to B C$ , where $B, C \in V - Σ - s$
  - $A \to a$ , where $a \in Σ$
Turing Machine and Undecidability
- Turing Machine 的表示
  - $M = (K, Σ, δ, s, H)$
  - $M_{\to}$ , $R_{⊔}$ , $L_{⊔}$ ...
- Recursive and recursively enumerable
  - $L$ is recursive
    - 构造 $M$ decides $L$ .
    - 构造 $L \leq_{R}$ known recursive languages.
  - $L$ is non-ecursive
    - 构造 known non-recursive language $\leq_{R} L$
      - 比如 $H$ , $R_{T M}$ , ${^{″} M_{1}^{″}^{″} M_{2}^{″} | L (M_{1}) = L (M_{2})}$
  - $L$ is recursively enumerable
    - 构造 $M$ semidecides $L$ .
    - 构造 $L \leq_{R}$ known recursive languages.
  - $L$ is non-recursivey enumerable
    - If $L$ is R.E, $\overset{―}{L}$ is R.E, thus $L$ is Recursive.
    - 构造 known non-recursively enumerable languages $\leq_{R} L$
      - known non-recursively enumerable languages 主要是 $\overset{―}{H}$
  - 规约技巧
    - 首先确定左边满足条件的情况和右边满足条件的情况，并进行适当的调整，比如 $M$ accepts $Σ^{*}$ 同样满足 $M$ accepts at least 2023 strings
    - 可以使用 for run M on w for |w| steps 进行情形的翻转
- Grammar
  - $(V, Σ, s, R)$
- Countable
- Numerical Function
  - primitive numerical function: basic func + composition + recursive definition
    - basic func
      - zero function: $z e r o (n_{1}, n_{2}, \dots, n_{k}) = 0$
      - identity function: $i d_{k, j} (n_{1}, n_{2}, \dots, n_{k}) = n_{j}$
      - successor function: $s u c c (n) = n + 1$
    - composition: $g (f (n))$
    - recursive definition: ${\begin{cases} f (n_{1}, \dots, n_{k}, 0) = g (n_{1}, \dots, n_{k}) \\ f (n_{1}, \dots, n_{k}, t + 1) = h (n_{1}, \dots, n_{k}, t, f (n_{1}, \dots, n_{k}, t)) \end{cases}$
  - $μ$ -recursive function: primitive numerical function + minimalization
    - minimalization $f (n_{1}, \dots, n_{k}) = {\begin{cases} m i n i m u m o f s u c h m & i f \exists m, g (n_{1}, \dots, n_{k}, m) = 1; \\ 0 & o t h e r w i s e . \end{cases}$

常见单词 / 术语

counterexample - 反例
composite number - 合数
symbols - 字符集
strings - 字符串
languages - 字符串的集合 / 语言
iambic string - 回文串
odd - 奇数
even - 偶数
automata - 自动机（单数形式 automaton）

Language

常见的 Language 及其属于的范畴

${a^{n} b^{n} | n \geq 0}$ 不是 Regular Language，是 CFL（可以使用 Pumping Theorem 证明）
${a^{n} b^{n} c^{n} | n \geq 0}$ 不是 CFL（可以使用 Pumping Theorem 证明），是 Recursive Language

运算符闭包性

Operator	Regular	Context-free	recursive	recursively enumerable
$\cup$	√	√	√	√
$\cap$	√	×	√	√
$\overset{―}{}$	√	×	√	×
$^{*}$	√	√	√	√
$^{\circ}$	√	√	√	√

Finite Automata and Regular Languages

Sequence of Configurations

Problem
Consider the following DFA. What sequence of configurations does the machine go through on input $a a b$ ?

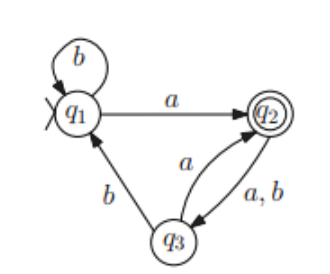
Solution

(q_{1}, a a b) ⊢_{M} (q_{2}, a b) ⊢_{M} (q_{3}, b) ⊢_{M} (q_{1}, e)

NFA ⇒ RL

解题思路

将 NFA 的起点和终点剥离出来
将中间状态依次等价转换
- 只关注 Simple Path 和 Simple Cycle
最终获得起点到终点的等价式

Problem
将以下的 NFA 转化为 RL

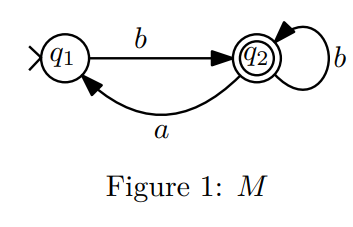
Solution

NFA ⇒ DFA

解题思路

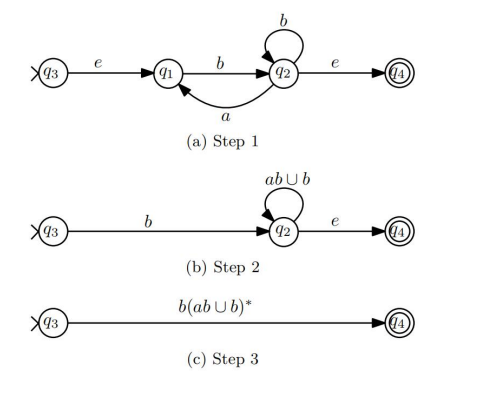
构造 $2^{|} K |$ 个状态的 DFA（不要忘记 $\emptyset$
建立转移关系
删除无用状态

Problem
Convert the following NFA to an equivalent DFA. Give only the portion of the DFA that is reachable from the initial state.

Answer

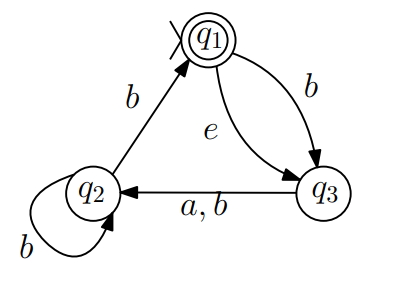
Prove languages are regular

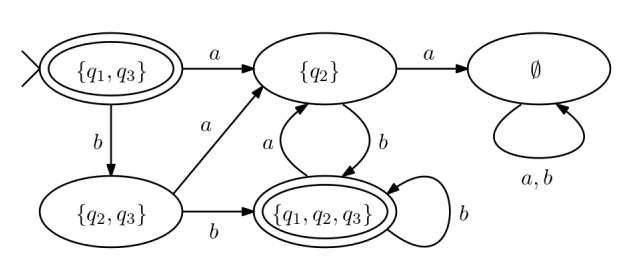
简单的 画出有限自动机即可；复杂的 构造 $(K, σ, δ, s, F)$ 就更好了

Problem1
The set of all binary strings that end with 00.
Solution1

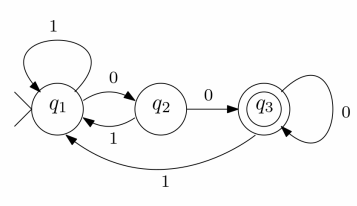
Problem2
Let $A$ and $B$ be two regular languages over some alphabet $Σ$ . Let $#$ be a symbol not in $Σ$ . Consider the following language.

L = {w_{1} # w_{2} : w_{1} \in A \land w_{2} \in B}

Solution2
Contruct a new FA $M_{3} = (K_{3}, Σ^{'}, δ_{3}, s_{3}, F_{3})$ as following.
（需要为接收到 # 的非法情况建立新的状态 $q_{0}$ ）

\begin{aligned} Σ^{'} = & Σ \cup {#} \\ K_{3} = & K_{1} \cup K_{2} \cup {q_{0}} \\ s_{3} = & s_{1} \\ F_{3} = & F_{2} \\ δ_{3} = & δ_{1} \cup δ_{2} \cup {((q, #), q_{0}) | q \in ((K_{1} - F_{1}) \cup K_{2})} \\ \cup {((q_{0}, a), q_{0}) | a \in Σ^{'}} \cup {((q^{'}, #), s_{2}) | q^{'} \in F_{1}} \end{aligned}

\emptyset

e

\emptyset^{*}

$\emptyset$ 是什么都没有的意思
$e$ 表示接受空串
$\emptyset^{*} \equiv e$
$R \emptyset = \emptyset$
$R \emptyset^{*} = R$
$R \cup \emptyset = R$

Construct NFA which accepts Regular Expressions

Problem
Construct a NFA that accepts $(a b \cup a b a)^{*}$ .

Solution

Regular Language

判断题：If $A$ is regular and $B$ is non-regular, then $A \circ B$ must be non-regular.
- 错误
- 反例： $A = \emptyset$ 的时候。
判断题：Language ${a^{i} b^{j} c^{k} | i, j, k \in N a n d i + j ≢ k \mod 3}$ is not regular.
- 错误
- 同余的情况只有有限种，可以拆封成类似 ${a^{3 i} b^{3 j} c^{3 k}}$ 的形式。
判断题：If $L_{1} \circ L_{2}$ is a regular language, then either $L_{1}$ or $L_{2}$ is regular.
- 错误
- 反例：Assume $A$ is non-regular ⇒ $\overset{―}{A}$ is non-regular ⇒ $A \cup {e}$ and $\overset{―}{A} \cup {e}$ are non-regular ⇒ $(A \cup {e}) \circ (\overset{―}{A} \cup {e}) = Σ^{*}$ is regular.

Pumping Theorem

Problem1
$L_{1} = {w t w | w, t \in {a, b}^{+}}$ is regular or not.
Solution1
Pumping Theorem.
假设 Pumping length 为 p，构造 $w = a^{p} b a a^{p} b = x y z \in L_{1}$ ,
因为 (2) |y|>0 (3) |xy≤p|，所以 $y = a^{i}$
则 $x y^{2} z = a^{n + i} b a a^{n} b \notin L_{2}$ （特别小心这里的判断）

Problem2
$L_{4} = {u v u^{R} | u, v \in {a, b}^{+}}$ is regular or not.
Solution2
注意 $L_{4}$ 其实只用判断首尾内容是否一致就行，故是正则的

Context Free Language

Suppose that

L

is context-free and

R

is regular, then

L - R

is context-free language.

正确。

$L - R = L \cap \overset{―}{R}$
$L$ is CFL, $\overset{―}{R}$ is RL, CFL $\cap$ RL = CFL
$L - R$ is CFL

CFL ⇒ CFG

Problem1
Construct a context-free grammar that generatesthe following language.

{x y \in {0, 1}^{*} : x h a s e q u a l n u m b e r o f 0^{'} s a n d 1^{'} s, a n d y = y^{R}}

Solution1
$S \to A B$
$A \to A A | 0 A 1 | 1 A 0 | e$
$B \to 0 B 0 | 1 B 1 | 0 | 1 | e$

Problem2
令 $L = {w \in {a, b}^{*} | a \neq b}$ ，试用 CFG 写出能表示 L 的文法

CFL ⇒ PDA

Problem
Construct a pushdown automaton that accepts the following language.

{w \in {a, b}^{*} : i n w, 2 \cdot # a = # b + 3}

Solution

\begin{aligned} P & = (K, Σ, Γ, Δ, s, F) \\ K & = {s, f} \\ Σ & = {a, b} \\ Γ & = {A, B} \\ s & = s \\ F & = {f} \end{aligned}

The list of $((q, α, β), (p, γ))$ shown below contains all elements in $Δ$

Parse tree

Problem
Consider the following context-free grammar.

\begin{aligned} E \to E + E \\ E \to E \times E \\ E \to a \end{aligned}

Show two distinct parse trees with root $E$ and yield $a \times a + a$
Solution

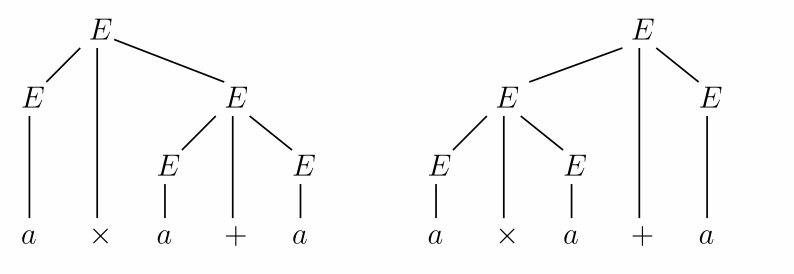
Turing Machine and Undecidability

Turing Machine

从基本定义出发构造图灵机

Problem

Solution

注意事项

图灵机之间状态转移时可能会出现不合法的情况

Design a right-shifting machine

S_{\leftarrow}

that transforms

▹ ⊔ w \underset{―}{⊔}

into

▹ ⊔ ⊔ w \underset{―}{⊔}

, where

w

is a string that contains no blank symbol.

Try to construct a Turing Machine to decide the following language.

L = {w w^{R} | w \in {0, 1}^{*}}

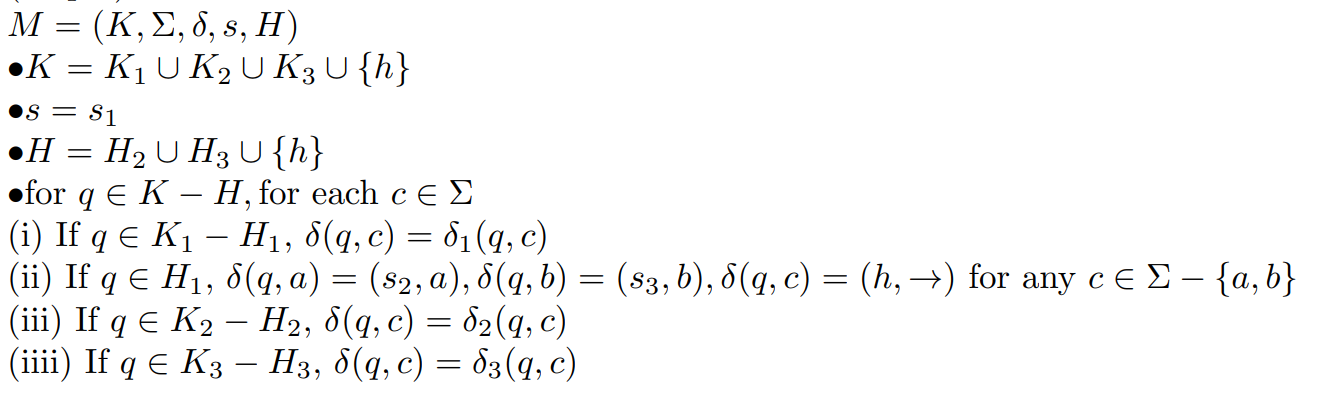
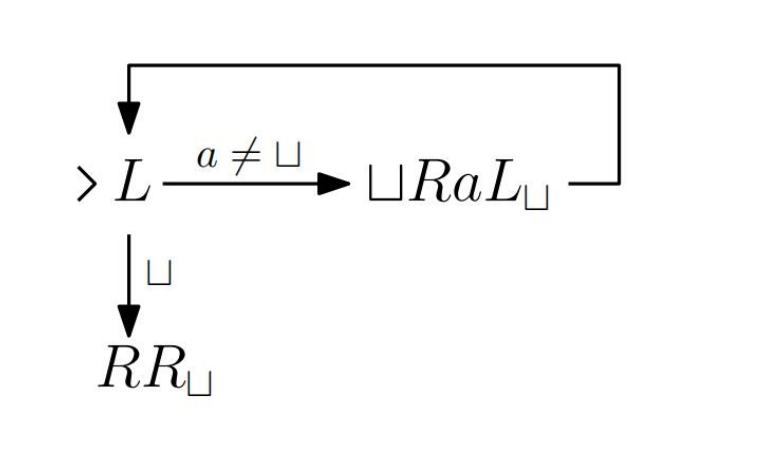
p.s. You can assume the start configuration of the Turing machine is $▹ \underset{―}{⊔} w$ .

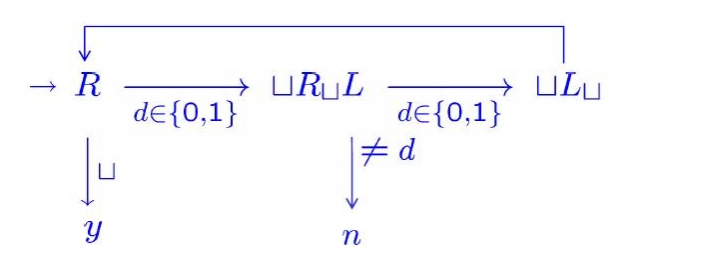
Undecidability

使用 Reduction 的基本定义

Problem
Let $A$ and $B$ be two languages. Suppose that we have a reduction $f$ from $A$ to $B$ . If $B$ is recursively enumerable, what conclusion can you draw about $A$ ?
Solution
$A$ is also recursively enumerable.
根据定义， $\forall w \in A$ if and only if $f (w) \in B$
对于 $M_{B}$ semidecides $B$ , 我们可以构造
M = on input $w$ , run $M_{B}$ on $f (w)$
则 $L (M) = A$ ，故 $A$ is recursively enumerable.

for

A \leq_{r} B

If $B$ is recursive, $A$ is recursive.
If $B$ is recursively enumerable, $A$ is recursively enumerable.
If $A$ is not recursive, $B$ is not recursive.
If $A$ is not recursively enumerable, $B$ is not recursively enumerable.

一些关于 Recursive 的判断题

判断题 1：If $A$ is recursive and $B \subseteq A$ , then $B$ is recursive as well.
回答：错误，因为 Recursive Language 的子集不一定 Recursive。
判断题 2：There's a function $ϕ$ such that $ϕ$ can be computed by some Turing machines, yet $ϕ$ is not a primitive recursive function.
回答：正确，因为 primitive recursive function 是 recursive function 的子集。

flowchart LR
	subgraph recursive function = μ-recursive function
		p[primitive recursive function]
	end

判断题 3：If $L_{1}, L_{2}$ , and $L_{3}$ are all recursively enumerable, then $L_{1} \cap (L_{2} \cup L_{3})$ must be recursively enumerable.
判断题 4：Let $L$ be a recursively enumerable language and $L \leq_{r} \overset{―}{H}$ , then $L$ is recursive, where $H$ = { “ $M$ ”“ $w$ ” | Turing machine $M$ halts on $w$ }.
回答：正确。因为 $\overset{―}{L} \leq_{r} H$ ⇒ $\overset{―}{L}$ is recursively enumerable ⇒ $L$ is recursive。 - 回答：正确，因为 Recursive Language 在 $\cup$ , $\cap$ 下封闭。

Let

L_{1}

and

L_{2}

be two recursively enumerable languages. If

L_{1} \cup L_{2}

and

L_{1} \cap L_{2}

are recursive, then both

L_{1}

and

L_{2}

are recursive.

正确。

Prove that every recursively enumerable language can be reduced to

H

构造 f(" $w$ ") = " $M$ "" $w$ "，即可证明 $L \leq_{r} H$ 。

Prove that the following language is not recursive. L = { "

M_{1}

" "

M_{2}

" "

k

M_{1}

and

M_{2}

are two Turing machines with

| L (M_{1}) \cap L (M_{2}) | \geq k

}

构造 f(" $M$ ") = " $M$ "" $M_{a l l}$ "" $1$ " ( $M_{a l l}$ 在所有输入下停机)
已知 A = { " $M$ ": $M$ halt on some inputs. } is not recursive.
$\forall M \in A$ , $| L (M) \cap L (M_{a l l}) | = | L (M) | \geq 1$ ⇒ $f (^{″} M^{″}) \in L$
$\forall M \notin A$ , $| L (M) \cap L (M_{a l l}) | = | L (M) | = | \emptyset | = 0$ ⇒ $f (^{″} M^{″}) \notin L$
$∴$ $A \leq_{r} L$
$∵$ $A$ is not recursive
$∴$ $L$ is not recursive

L_{e v e n}

= { "

M

" |

M

is a TM and

L (M)

contains at least one string of even number of

b

's }

(1) Show that $L_{e v e n}$ is recursively enumerable.
Constrcut $M_{A}$ = on input " $M$ "

for i = 1, 2, 3, ...
	// 将满足 even number of b's 的字符串按字典序枚举
	for s = s1, s2, s3, ..., si 
		run M on s for i steps
		if M halts on s within i steps
			halt

(2) Show that $L_{e v e n}$ is non-recursive.
答：使用 Rice's Theorem
构造 f("M""w") = on input $v$
step1 run $M$ on $w$
step2 run $M_{A}$ on $v$ , where $M_{A}$ accepts string $b$ .
当 $^{″} M^{″}^{″} w^{″} \in H$ 时， $L [f (^{″} M^{″}^{″} w^{″})] = L (M_{A})$ ⇒ $f (^{″} M^{″}^{″} w^{″}) \in L_{e v e n}$
当 $^{″} M^{″}^{″} w^{″} \notin H$ 时， $L [f (^{″} M^{″}^{″} w^{″})] = \emptyset$ ⇒ $f (^{″} M^{″}^{″} w^{″}) \notin L_{e v e n}$
所以 $H \leq_{R} L_{e v e n}$ ， $L_{e v e n}$ is non-recursive

Classify whether each of the following languages are recursive, recursively enumerable but not recursive, or non-recursively enumerable.

(1) The language $A L$ = {" $M$ " | TM $M$ accepts at least 2018 strings.}
首先， $A L$ 递归可枚举，可以构造如下自动机

Constrcut $M_{A}$ = on input " $M$ "

for i = 1, 2, 3, ...
	count = 0
	for s = s1, s2, s3, ..., si
		run M on s for i steps
		if M halts on s within i steps
			count = count + 1
	if count >= 2023
		halts

其次， $A L$ 非递归，可进行如下归约 $H \leq A L$

Contruct f("M""w") = on input v
step1 run $M$ on $w$
step2 run $M_{A}$ on $v$ which accepts everything

当 $^{″} M^{″}^{″} w^{″} \in H$ 时， $| L [f (^{″} M^{″}^{″} w^{″})] | = | L (M_{A}) | \geq 2018$ ⇒ $f (^{″} M^{″}^{″} w^{″}) \in A L$
当 $^{″} M^{″}^{″} w^{″} \notin H$ 时， $| L [f (^{″} M^{″}^{″} w^{″})] | = | \emptyset | = 0$ ⇒ $f (^{″} M^{″}^{″} w^{″}) \notin A L$
所以 $H \leq_{R} A L$ , $A L$ is non-recursive

(2) The language $E$ = {" $M$ " | TM $M$ accepts at exactly 2018 strings.}
$E$ 非递归可枚举

Contruct f("M""w") = on input v
if $v = u_{i}$ then halt// $u_{1}, \dots, u_{2018}$ 是事先规定好的 2018 个串
else run M on w

当 $^{″} M^{″}^{″} w^{″} \in \overset{―}{H}$ 时， $| L (f (^{″} M^{″}^{″} w^{″})) | = 2018$ ⇒ $f (^{″} M^{″}^{″} w^{″}) \in E$
当 $^{″} M^{″}^{″} w^{″} \notin \overset{―}{H}$ 时， $| L (f (^{″} M^{″}^{″} w^{″})) | = \infty > 2018$ ⇒ $f (^{″} M^{″}^{″} w^{″}) \notin E$

(3) The language $A M$ = {" $M$ " | TM $M$ accepts at most 2018 strings.}
$A M$ 时非递归可枚举的，可以使用反证法。
若 $A M$ 递归可枚举，由 (1) 知 $\overset{―}{A M}$ 也递归可枚举，则 $A M$ 和 $\overset{―}{A M}$ 递归，又因为 $\overset{―}{A M}$ 非递归，故矛盾。

Grammar

Contruct a grammar that generates

{w w : w \in {a, b}^{*}}

V = { S, S', T, A, B, a, b }, $Σ$ = { a, b }, R is the set of the following rules
S → TS'
S' → AaS' | BbS' | e
aA → Aa
aB → Ba
bA → Ab
bB → Bb
TA → aT
TB → bT
T → e

Numerical Function

Show that the function:

φ : N \to N

given by

ϕ (x) = {\begin{cases} x \mod 3, & i f x i s a c o m p o s i t e n u m b e r; \\ x^{2} + 1, & o t h e r w i s e . \end{cases}

is primitive recursive.

Since

φ (x) = r e m (x, 3) \cdot (1 \sim p r i m e (x)) + (x^{2} + 1) \cdot p r i m e (x)

and $r e m (x, 3)$ , $x^{2} + 1$ are primitive recursive functions, $p r i m e (x)$ is a primitive recursive predicate, hence $φ (x)$ is primitive recursive.

Show the following function

ϕ_{k} : \underset{k}{\underset{⏟}{N \times N \times \dots \times N}} \to N

, and

k \in N, k \geq 2

ϕ_{k} (n_{1}, n_{2}, \dots, n_{k}) = max_{k} {n_{1}, n_{2}, \dots, n_{k}}

is primitive recursive.

使用 recursive definition 推导

构造 ${\begin{cases} f (n_{1}, \dots, n_{k}, 0) = g (n_{1}, \dots, n_{k}) \\ f (n_{1}, \dots, n_{k}, t + 1) = h (n_{1}, \dots, n_{k}, t, f (n_{1}, \dots, n_{k}, t)) \end{cases}$
证明 $g$ 和 $h$ 均为原始递归函数

令 $f (n_{1}, n_{2}, \dots, n_{k}, k) = max {n_{1}, n_{2}, \dots, n_{k}}$

f (n_{1}, n_{2}, \dots, n_{k}, 0) = max_{2} {n_{1}, n_{2}} = n_{1} \cdot (n_{1} > n_{2}) + n_{2} \cdot (n_{2} \leq n_{1})

f (n_{1}, n_{2}, \dots, n_{k}, k) = max {n_{1}, n_{2}, \dots, n_{k}} = max_{2} {f (n_{1}, n_{2}, \dots, n_{k - 1}, k - 1), n_{k}}

所以 $f (n_{1}, n_{2}, \dots, n_{k}, k)$ 是原始递归函数
所以 $φ_{k} (n_{1}, n_{2}, \dots, n_{k})$ 是原始递归函数

Countable

Countable 相关问题

Problem1
Prove that every language is countable.
Solution1
$∵$ $Σ^{*}$ is countable and a subset of a countable set is countable.
$∴$ $L \subseteq Σ^{*}$ is countable.

Problem2
Prove that there is an undecidable subset of ${1}^{*}$ .
Solution2
$∵$ Every language is countable
$∴$ The recursive languages is countable.
$∵$ The power set of ${1}^{*}$ is uncountable.
$∴$ There is an uncountable subset of ${1}^{*}$

Problem3
Prove that the set of undecidable languages is uncountable.
Solution3
$∵$ The set of Turing Machine is countable.
$∴$ The set of decidable languages is countable.
$∴$ The set of undecidable languages is uncountable.

Problem4
Prove that countable does not imply Turing enumerable(recursively enumerable)
Solution4
$∵$ All the language is enumerable and not all the language is recursively enumerable, like $\overset{―}{H}$
$∴$ There exists languages(must be countable) which are not recursively enumerable.